Srednješolsko tekmovanje ACM iz računalništva in informatike

Barvanje mreže

To je „off-line naloga“. Na tej spletni strani je objavljen opis naloge in testni primeri. Svoje rešitve lahko pošlješ prek obrazca na tej strani kadarkoli do vključno 27. marca 2026 (dan pred tekmovanjem).

• Kratek opis naloge na tej strani.
• Podroben opis naloge in oblike vhodnih ter izhodnih datotek.
• Vhodne datoteke.
• Registracija (preden lahko oddajaš svoje rešitve).
• Obrazec za oddajo tvojih rešitev.
• Najboljši doslej oddani rezultati za posamezni testni primer.
• Razvrstitev tekmovalcev v skupnem seštevku.

Opis naloge

Dana je karirasta mreža n × n polj. Posamezno polje je lahko belo, črno ali rdeče. Rekli bomo, da sta si polji (x₁, y₁) in (x₂, y₂) bližnji, če velja |x₁ − x₂| ≤ d in |y₁ − y₂| ≤ d. Polja ne štejemo za bližnje samemu sebi.

Mreža je veljavna, če ima vsako črno polje vsaj b bližnjih belih polj in kvečjemu c bližnjih črnih polj. Zagotovljeno je, da je mreža v začetnem stanju, kot ga dobimo v vhodnih podatkih, veljavna. Naša naloga je spremeniti nekaj belih polj v črna tako, da mreža ostane veljavna in da bo v mreži čim več parov bližnjih črnih polj.

Primer: recimo, da imamo n = 6, d = 1, b = 1 in c = 5. Naslednja slika kaže nekaj primerov mrež. Prva je vhodna mreža, ostale lahko dobimo iz nje tako, da nekaj belih polj pobarvamo črno.

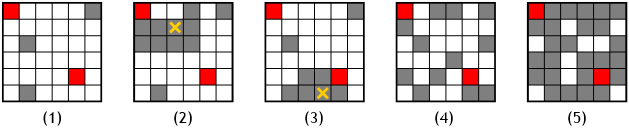
1. vhodna mreža (veljavna);
2. neveljavna mreža: neko črno polje (označeno s križcem) ima preveč bližnjih črnih polj;
3. neveljavna mreža: neko črno polje (označeno s križcem) ima premalo bližnjih belih polj;
4. veljavna mreža, na njej je 6 parov bližnjih črnih polj;
5. veljavna mreža, na njej je 49 parov bližnjih črnih polj.

Mreži (4) in (5) sta torej obe veljavni rešitvi za vhodno mrežo (1), vendar je (5) veliko boljša rešitev kot (4).

• Podrobnejši opis naloge ter vhodnih in izhodnih datotek.
• Vhodne datoteke.
• Registracija.

Obrazec za oddajo rešitev

(Oddaja rešitev je možna do vključno 27. marca 2026.)

Datoteka s tvojo rešitvijo:

Najboljše doslej oddane rešitve

Skupni seštevek

V skupnem seštevku se za vsakega tekmovalca seštejejo njegove točke z vseh testnih primerov.

Ime in priimek	Rezultat
Matej Kralj	109
samo Kralj	101
Jakob Ferjančič	79
Anže Hočevar	77
Domen Koder	48
Xander Bizjak	40
Luka Stražišar	35
Gregor Kikelj	28
David Cimerman-Marjanovič	27
Vid Furlan	25
Andrej Golčer	12

Pripis: rezultatov psevdonimnih tekmovalcev v gornji tabeli ne bomo prikazovali. Če bi se kateri od njih vendarle želel pojaviti v tabeli, naj mi po elektronski pošti pošlje svoje ime in šestmestno številko, pod katero je oddajal svoje rešitve.

[H kazalu. | Na vrh te strani. | Imate vprašanje ali komentar?]