Srednješolsko tekmovanje ACM iz računalništva in informatike

Barvanje mreže

Podroben opis naloge

Dana je karirasta mreža n × n polj. Posamezno polje je lahko belo, črno ali rdeče. Položaj polja lahko opišemo s parom koordinat (x, y), pri čemer x pomeni številko stolpca (od 1 na levi do n na desni), y pa številko vrstice (od 1 na vrhu mreže do n na dnu).

Rekli bomo, da sta si polji (x₁, y₁) in (x₂, y₂) bližnji, če velja |x₁ − x₂| ≤ d in |y₁ − y₂| ≤ d. Polja ne štejemo za bližnje samemu sebi.

Mreža je veljavna, če ima vsako črno polje vsaj b bližnjih belih polj in kvečjemu c bližnjih črnih polj. Zagotovljeno je, da je mreža v začetnem stanju, kot ga dobimo v vhodnih podatkih, veljavna. Naša naloga je spremeniti nekaj belih polj v črna tako, da mreža ostane veljavna in da bo v mreži čim več parov bližnjih črnih polj.

Primer: recimo, da imamo n = 6, d = 1, b = 1 in c = 5. Naslednja slika kaže nekaj primerov mrež. Prva je vhodna mreža, ostale lahko dobimo iz nje tako, da nekaj belih polj pobarvamo črno.

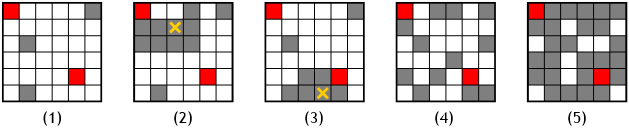
vhodna mreža (veljavna);
neveljavna mreža: neko črno polje (označeno s križcem) ima preveč bližnjih črnih polj;
neveljavna mreža: neko črno polje (označeno s križcem) ima premalo bližnjih belih polj;
veljavna mreža, na njej je 6 parov bližnjih črnih polj;
veljavna mreža, na njej je 49 parov bližnjih črnih polj.

Mreži (4) in (5) sta torej obe veljavni rešitvi za vhodno mrežo (1), vendar je (5) veliko boljša rešitev kot (4).

Ocenjevalni program

Lahko si preneseš izvorno kodo programa, s katerim bomo ocenjevali prejete rešitve: Rtk26Barvanje.cpp.

Na voljo je tudi prevedena različica ocenjevalnega programa (za Windows).

Oblika vhodne datoteke

Pri tej nalogi so vsi testni primeri podani v eni vhodni datoteki. V prvi vrstici vhodne datoteke je niz z imenom naloge (Barvanje), v drugi pa število testnih primerov (T). Sledijo testni primeri, pred vsakim od njih pa je še ena prazna vrstica.

Vsak testni primer se začne z vrstico, ki vsebuje številko tega testnega primera (od 1 do T). Sledi vrstica s števili n, d, b in c, ločenimi s po enim presledkom. Sledi n vrstic, ki podajajo začetno stanje mreže. Vsaka od teh vrstic vsebuje n znakov (brez presledkov), ki predstavljajo barve polj v tisti vrstici mreže. Bela polja so predstavljena s pikami, rdeča s črko R, črna pa z znakom #.

Primer: če bi imeli en sam testni primer, in sicer tistega iz slike v opisu naloge zgoraj, bi bila vhodna datoteka lahko takšna:

Barvanje
1

1
6 1 1 5
R....#
......
.#....
......
....R.
.#....

V resnici je pri tej nalogi 12 testnih primerov; velikosti mreže pri njih so n = 30, 100, 300 in 1000 (za vsako velikost so po trije testni primeri).

Oblika izhodne datoteke

Oddaš lahko poljubno število izhodnih datotek s svojimi rešitvami. Pri tem vsaka izhodna datoteka vsebuje rešitve za enega ali več testnih primerov. Če za isti testni primer oddaš več rešitev, bomo pri ocenjevanju upoštevali najboljšo med njimi.

Oblika posamezne izhodne datoteke je naslednja:

V prvi vrstici naj bo koda, ki si jo dobil(a) ob registraciji in iz katere je razvidno, da si rešitev res poslal(a) ti, ne pa kdo drug. V drugi vrstici naj bo ime naloge (Barvanje). Sledijo naj tvoje rešitve za enega ali več testnih primerov.

Vsaka rešitev se začne s prazno vrstico. Sledi naj vrstica, ki vsebuje številko testnega primera (od 1 do T), na katerega se ta rešitev nanaša. Sledi naj n vrstic, od katerih naj vsaka vsebuje n znakov, ki opisujejo stanje mreže po tistem, ko si nekaj belih polj pobarval črno. Barve naj bodo predstavljene enako kot v vhodni datoteki: pika pomeni belo polje, črka R rdeče in znak # črno.

Pazi na to, da morajo polja, ki so bila črna ali rdeča že v vhodni mreži, ostati enake barve tudi v tvoji izhodni mreži; polja pa, ki so bila v vhodni mreži bela, so lahko v tvoji izhodni mreži bela ali črna (ne smejo pa biti rdeča). Poleg tega mora imeti v tvoji izhodni mreži vsako črno polje vsaj b bližnjih belih polj in kvečjemu c bližnjih črnih polj.

Primer izhoda: če bi bila naša uporabniška koda enaka 123456 in bi obstajal testni primer št. 1, kakršen je prikazan zgoraj, bi lahko oddali spodnjo izhodno datoteko.

123456
Barvanje

1
R#####
##.##.
.##..#
##.###
##.#R#
.####.

To je mreža (5) s slike v opisu naloge.

Ocenjevanje

Rešitve (pri posameznem testnem primeru) se razvrsti po številu parov bližnjih črnih polj (več je bolje).

Rešitev, ki ne ustreza zgoraj opisanim pravilom za obliko in vsebino izhodne datoteke, je neveljavna in se ne bo upoštevala.

Vhodni podatki

barvanje.in — datoteka z vsemi vhodnimi podatki za to nalogo.
barvanje-unix.in — ista datoteka, vendar z unixaškimi konci vrstic (LF namesto CRLF).

Registracija

Preden lahko oddajaš svoje rešitve, se prijavi prek spodnjega obrazca. Dodelili ti bomo enolično uporabniško kodo, ki jo boš potreboval(a) za pripravo svojih izhodnih datotek.

Opomba: pri tej nalogi lahko sodeluje kdorkoli, ne glede na starost, izobrazbo, itd. Objavili bomo rezultate vseh tekmovalcev, za morebitne praktične nagrade pa pridejo v poštev le srednješolci/ke in študentje/ke.

Obrazec za oddajo rešitev

(Oddaja rešitev je možna do vključno 27. marca 2026.)

[Nazaj na glavno stran. | Na vrh te strani. | Imate vprašanje ali komentar?]

Ime in priimek:	*
e-mail:	*
Šola:
Letnik:
Mentor: