Srednješolsko tekmovanje ACM iz računalništva in informatike

Zlaganje krogov

Podroben opis naloge

Danih je n krogov s polmeri r₁, r₂, …, r_n. Tvoja naloga je razporediti te kroge po ravnini tako, da bodo njihova središča vsa ležala na enotskem kvadratu, krogi pa se bodo čim manj prekrivali. To pomeni, da moraš za vsak krog i (od 1 do n) izbrati koordinati njegovega središča (x_i, y_i), ki morata ležati na intervalu 0 ≤ x_i ≤ 1 in 0 ≤ y_i ≤ 1.

Tvoj razpored (nabor koordinat središč vseh n krogov) bomo ocenili tako, da bomo za vsak par krogov izračunali ploščino njunega preseka in to sešteli po vseh parih krogov:

cena = Σ_{i = 2, …, n} Σ_{j = 1, …, i − 1} Presek(x_i, y_i, r_i, x_j, y_j, r_j),

pri čemer Presek(…) pomeni ploščino preseka kroga s središčem (x_i, y_i) in polmerom r_i ter kroga s središčem (x_j, y_j) in polmerom r_j. (Več o tem, kako računati presek krogov.) Rešitev je tem boljša, čim manjša je vsota cena iz gornje formule.

Kot vidimo iz gornje formule, se ploščina območja, kjer se prekriva več krogov, šteje po večkrat; natančneje rečeno, če se na nekem območju prekriva natanko k krogov, se ploščina tega območja šteje kar k · (k − 1)/2-krat.

Primer: recimo, da moramo razporediti štiri kroge s polmeri 1/10, 1/5, 1/2 in 7/10. Naslednja slika kaže tri primere takšnih razporedov (možnih je seveda še neskončno mnogo drugih razporedov). Črne pike so središča krogov; pobarvana so območja, kjer se krogi prekrivajo (modra = prekrivata se natanko dva kroga; zelena = prekrivajo se natanko trije krogi; rdeča = prekrivajo se vsi štirje krogi); črtkane črte označujejo enotski kvadrat.

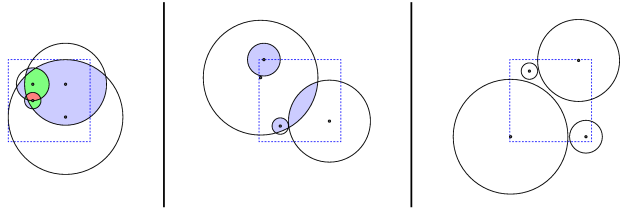
Prva od teh rešitev je zelo slaba, saj se krogi močno prekrivajo. Druga je že veliko boljša, tretja pa je optimalna, saj se krogi pri njej sploh ne prekrivajo več. (V splošnem seveda ni nujno, da je dane kroge sploh mogoče razporediti tako, da se ne prekrivajo; za tale konkretni nabor štirih krogov pa je to vendarle mogoče.)

Opozorimo še, da (kot vidimo tudi iz primerov na sliki) morajo v enotskem kvadratu ležati le središča krogov, drugače pa ni nič narobe, če krogi delno štrlijo iz enotskega kvadrata.

Ocenjevalni program

Lahko si preneseš izvorno kodo programa, s katerim bomo ocenjevali prejete rešitve: Rtk25Zlaganje.cpp.

Na voljo je tudi prevedena različica ocenjevalnega programa (za Windows).

Oblika vhodne datoteke

Pri tej nalogi so vsi testni primeri podani v eni vhodni datoteki. V prvi vrstici vhodne datoteke je niz z imenom naloge (Zlaganje), v drugi pa število testnih primerov (T). Sledijo testni primeri, pred vsakim od njih pa je še ena prazna vrstica.

Vsak testni primer se začne z vrstico, ki vsebuje številko tega testnega primera (od 1 do T). Sledi vrstica s številom n, ki pove, koliko krogov nastopa v tem testnem primeru. Sledi n vrstic, od katerih i-ta vsebuje število r_i, torej polmer i-tega kroga pri tem testnem primeru. Zanj bo veljalo 0 < r_i ≤ 2.

Primer: če bi imeli en sam testni primer, in sicer tistega iz slike v opisu naloge zgoraj, bi bila vhodna datoteka lahko takšna:

Zlaganje
1

4
0.1
0.2
0.5
0.7

~~V resnici je pri tej nalogi 10 testnih primerov. Pri večini primerov je krogov nekaj deset, le pri enem (največjem) jih je malo čez 200.~~ Pozor: prvotnih deset testnih primerov se je izkazalo za malo prelahkih, zato smo objavili še deset težjih. Skupaj je torej zdaj pri tej nalogi dvajset testnih primerov (največji ima 703 kroge).

Oblika izhodne datoteke

Oddaš lahko poljubno število izhodnih datotek s svojimi rešitvami. Pri tem vsaka izhodna datoteka vsebuje rešitve za enega ali več testnih primerov. Če za isti testni primer oddaš več rešitev, bomo pri ocenjevanju upoštevali najboljšo med njimi.

Oblika posamezne izhodne datoteke je naslednja:

V prvi vrstici naj bo koda, ki si jo dobil(a) ob registraciji in iz katere je razvidno, da si rešitev res poslal(a) ti, ne pa kdo drug. V drugi vrstici naj bo ime naloge (Zlaganje). Sledijo naj tvoje rešitve za enega ali več testnih primerov.

Vsaka rešitev se začne s prazno vrstico. Sledi naj vrstica, ki vsebuje številko testnega primera (od 1 do T), na katerega se ta rešitev nanaša. Sledi naj n vrstic, od katerih naj i-ta vsebuje števili x_i in y_i (torej koordinati središča i-tega kroga; to je tisti s polmerom r_i), ločeni s presledkom. Za koordinati mora veljati 0 ≤ x_i ≤ 1 in 0 ≤ y_i ≤ 1.

Primer izhoda: če bi bila naša uporabniška koda enaka 123456 in bi obstajal testni primer št. 1, kakršen je prikazan zgoraj, bi lahko oddali spodnjo izhodno datoteko.

123456
Zlaganje

1
0.26 0.19
0.6 1
0.86 0.25
0.02 0.78

To je drugi razpored s slike v opisu naloge.

Ocenjevanje

Rešitve (pri posameznem testnem primeru) se razvrsti po ceni, izračunani po formuli v opisu naloge (manjša je boljša). Spomnimo se, da dobimo to ceno tako, da za vsak par krogov izračunamo ploščino njunega preseka in te ploščine seštejemo po vseh parih krogov.

Rešitev, ki ne ustreza zgoraj opisanim pravilom za obliko in vsebino izhodne datoteke, je neveljavna in se ne bo upoštevala.

Formula za presek dveh krogov

Da se ne bo komu naloga zdela preveč matematična, lahko tukaj skupaj razmislimo o tem, kako računati ploščino preseka dveh krogov. Recimo, da imamo krog s središčem A in polmerom r ter krog s središčem B in polmerom R (glej spodnjo sliko). Razdaljo med središčema označimo z d = |AB|.

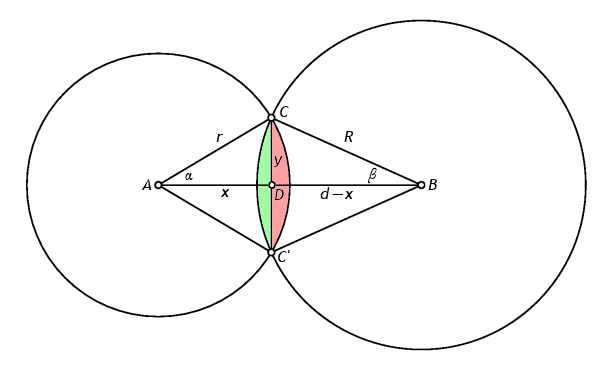
Postavimo v mislih koordinatno izhodišče v točko A in zasukajmo osi tako, da ima B (torej središče drugega kroga) koordinati (d, 0). Točke na prvi krožnici potem ustrezajo enačbi x² + y² = r², tiste na drugi krožnici pa enačbi (d − x)² + y² = R². Če odštejemo prvo enačbo od druge, dobimo d² − 2dx = R² − r², iz tega pa izrazimo x = (d² − R² + r²) / (2d). Tako smo dobili x-koordinato presečišč, nato pa s pomočjo enačbe prve krožnice izračunamo še y-koordinato: y = ± √(r² − x²). Na sliki sta presečišči označeni s C in C′.

Trikotnik △ACC′ je enakokrak; če ga razpolovimo, dobimo pravokotni trikotnik △ADC s katetama x in y ter hipotenuzo r. Kót pri točki A označimo z α = ∠CAD. Vidimo, da je tg α = y/x, torej α = arc tg(y/x).

Krožni izsek, ki ga v levem krogu omejujeta daljici AC in AC', ima v vrhu kot 2α, torej ima ploščino αr². Če od nje odštejemo ploščino trikotnika △ACC′ (to pa je x · y), dobimo ploščino krožnega odseka, ki je na sliki pobarvan rdeče. Ta ploščina je torej αr² − xy.

Podoben razmislek za desni krog bi nam pokazal, da je ploščina zelenega odseka enaka βR² − (d − x)y za β = ∠CBD = arc tg(y/(d − x)). Vsota obeh odsekov, rdečega in zelenega, pa je ravno presek obeh krogov.

Primer implementacije tega izračuna v C++:

#include <cmath>
#include <algorithm>
using namespace std;

const double eps = 1e-8, pi = 4 * atan(1);

// Vrne ploščino tistega dela kroga s središčem (0, 0) in polmerom r,
// ki leži desno od dane x-koordinate.
double KrozniOdsek(double x, double r)
{
    if (x >= r - eps) return 0;
    if (x <= -r + eps) return pi * r * r;
    double y = sqrt(r * r - x * x);
    double alfa = atan2(y, x);
    double izsek = alfa * r * r;
    return izsek - x * y;
}

// Vrne ploščino preseka krogov s polmeroma r in R,
// če je razdalja med njunima središčema enaka d.
double PresekKrogov(double r, double R, double d)
{
    // Če sta si središči oddaljeni za vsaj r + R, se kroga sploh ne sekata.
    if (d >= r + R - eps) return 0;
    // Če imata kroga skupno središče, je presek enak ploščini manjšega kroga.
    if (d < eps) return pi * min(r, R) * min(r, R);
    double x = (d * d - R * R + r * r) / (2 * d);
    return KrozniOdsek(x, r) + KrozniOdsek(d - x, R);
}

In še primer implementacije v pythonu:

import math

eps = 1e-8

# Vrne ploščino tistega dela kroga s središčem (0, 0) in polmerom r,
# ki leži desno od dane x-koordinate.
def KrozniOdsek(x, r):
    if x >= r - eps: return 0
    if x <= -r + eps: return math.pi * r * r
    y = math.sqrt(r * r - x * x)
    alfa = math.atan2(y, x)
    izsek = alfa * r *r
    return izsek - x * y

# Vrne ploščino preseka krogov s polmeroma r in R,
# če je razdalja med njunima središčema enaka d.
def PresekKrogov(r, R, d):
    # Če sta si središči oddaljeni za vsaj r + R, se kroga sploh ne sekata.
    if d >= r + R - eps: return 0
    # Če imata kroga skupno središče, je presek enak ploščini manjšega kroga.
    if d < eps: return math.pi * min(r, R) * min(r, R);
    x = (d * d - R * R + r * r) / (2 * d)
    return KrozniOdsek(x, r) + KrozniOdsek(d - x, R)

Za vajo lahko sami razmislite, da daje opisani postopek pravilne rezultate tudi v primerih, ko odsek pokriva več kot polovico kroga ali pa ko en krog celo leži v drugem.

Vhodni podatki

Pozor: prvotnih deset testnih primerov se je izkazalo za malo prelahkih, zato smo zdaj objavili novo različico vhodne datoteke, v kateri je dvajset primerov (prvih deset je enakih kot prej, drugih deset pa je novih in malo težjih).

zlaganje.in — datoteka z vsemi vhodnimi podatki za to nalogo.
zlaganje-unix.in — ista datoteka, vendar z unixaškimi konci vrstic (LF namesto CRLF).

Registracija

Preden lahko oddajaš svoje rešitve, se prijavi prek spodnjega obrazca. Dodelili ti bomo enolično uporabniško kodo, ki jo boš potreboval(a) za pripravo svojih izhodnih datotek.

Opomba: pri tej nalogi lahko sodeluje kdorkoli, ne glede na starost, izobrazbo, itd. Objavili bomo rezultate vseh tekmovalcev, za morebitne praktične nagrade pa pridejo v poštev le srednješolci/ke in študentje/ke.

Obrazec za oddajo rešitev

(Oddaja rešitev je možna do vključno 21. marca 2025.)

[Nazaj na glavno stran. | Na vrh te strani. | Imate vprašanje ali komentar?]

Ime in priimek:	*
e-mail:	*
Šola:
Letnik:
Mentor: