Srednješolsko tekmovanje ACM iz računalništva in informatike
Zlaganje likov
- Objavili smo vhodne podatke, deluje tudi oddajanje in ocenjevanje rešitev. Format vhodnih in izhodnih datotek je malo drugačen, kot je bil doslej objavljen na tej strani, zato reševalcem priporočamo, da si še enkrat preberejo opis formata datotek na tej strani.
Podroben opis naloge
Dano je veliko število likov iz igre Tetris. Naloga je zložiti like v večji lik s čim manjšim obsegom, pri čemer se liki med seboj ne smejo prekrivati. Možne oblike likov so naslednje:
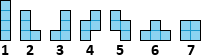
Kot vhodne podatke dobimo sedem celih števil, n1, …, n7, ki nam povedo, koliko likov posamezne oblike imamo.
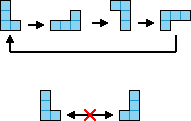
Like zlagamo na karirasto mrežo, pri čemer se ne smejo prekrivati. Lahko jih vrtimo v korakih po 90 stopinj okoli osi, ki je pravokotna na ravnino, v kateri ležijo; ne smemo pa jih obračati okoli osi, vzporedne s to ravnino:
Naša naloga je zložiti te like tako, da nastane nov lik s čim manjšim obsegom. Pri tem je novi „lik” lahko tudi sestavljen iz več nepovezanih delov, lahko vsebuje luknje ipd. Obseg je definiran kot skupna dolžina vseh robov, pri katerih liki mejijo na belo podlago naše kariraste mreže (namesto na druge like).
Primer: recimo, da imamo n2 = 2, n5 = n6 = n7 = 1 in n1 = n3 = n4 = 0; z drugimi besedami, recimo, da imamo naslednje like:
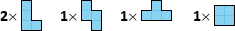
Teh pet likov lahko zložimo na veliko različnih načinov in dosežemo različno velike obsege. Spodnja slika prikazuje tri izmed njih in pod vsakim še njegov obseg:
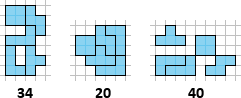
Med temi tremi razporedi je torej najboljši tisti v sredini, ki ima obseg samo 20 enot.
Ocenjevalni program
Lahko si preneseš izvorno kodo programa, s katerim bomo ocenjevali prejete rešitve: Rtk13Zlaganje.cpp.
Na voljo je tudi prevedena različica ocenjevalnega programa (za Windows).
Oblika vhodne datoteke
Pri tej nalogi so vsi testni primeri podani v eni vhodni datoteki. V prvi vrstici vhodne datoteke je niz z imenom naloge (Zlaganje), v drugi pa število testnih primerov (N). Sledi po ena vrstica za vsak testni primer. Vsaka od teh vrstic vsebuje osem celih števil, ločenih s po enim presledkom: najprej številko testnega primera (od 1 do N), nato pa po vrsti števila n1, n2, …, n7. Ta števila povedo, koliko likov posamezne vrste imamo. Vsako od njih je večje ali enako 0 in manjše ali enako 300.
Primer: če bi imeli en sam testni primer, in sicer tistega z gornje slike, bi bila vhodna datoteka takšna:
Zlaganje 1 1 0 2 0 0 1 1 1
V resnici bo pri tej nalogi 300 testnih primerov; za ilustracijo je tule prvih in zadnjih nekaj vrstic prave vhodne datoteke:
Zlaganje 300 1 1 283 28 0 24 0 203 2 1 0 6 257 1 27 240 3 0 267 0 0 0 0 213 4 292 20 1 24 0 28 21 ... 298 0 23 20 223 0 250 6 299 0 0 83 291 0 0 26 300 159 69 269 35 91 53 4
Oblika izhodne datoteke
Oddaš lahko poljubno število izhodnih datotek s svojimi razporedi likov. Pri tem vsaka izhodna datoteka vsebuje rešitve (razporede) za enega ali več testnih primerov. Če za isti testni primer oddaš več razporedov, bomo pri ocenjevanju upoštevali najboljšega med njimi.
Oblika posamezne izhodne datoteke je naslednja:
V prvi vrstici naj bo koda, ki si jo dobil(a) ob registraciji in iz katere je razvidno, da si rešitev res poslal(a) ti, ne pa kdo drug. V drugi vrstici naj bo ime naloge (Zlaganje). Sledijo naj tvoje rešitve za enega ali več testnih primerov.
Vsaka rešitev se začne s prazno vrstico. V drugi vrstici naj bo številka testnega primera, na katerega se nanaša ta rešitev. V tretji vrstici naj bosta dve celi števili, w in h (ločeni z enim presledkom), ki povesta širino in višino mreže, v katero so pri tej rešitvi zloženi vhodni liki. Pri tem mora veljati 1 ≤ w ≤ 104, 1 ≤ h ≤ 104 in 1 ≤ w · h ≤ 105.
Sledi naj h vrstic, ki opisujejo stanje mreže; vsaka od teh vrstic naj vsebuje w nenegativnih celih števil, ločenih s presledkom, ki opisujejo posamezna polja. Pri tem število 0 pomeni, da je pripadajoče polje prazno; pozitivno število pa pove, kateri od n1 + n2 + … + n7 vhodnih likov leži na tem polju mreže.
Pri tem je vseeno, v kakšnem vrstnem redu oštevilčiš vhodne like; celo ni nujno, da po vrsti uporabljaš števila od 1 naprej (morajo pa biti vsa uporabljena števila manjša od 109). Dopustno je celo, da isto številko uporabiš za več vhodnih likov. Omejitev je le ta, da če v tvojem razporedu dva lika mejita eden na drugega (imata kakšen skupen rob), potem ne smeta imeti iste številke. Poleg tega mora seveda za vsak lik veljati, da imajo vsa štiri polja, ki jih ta lik pokriva, isto številko.
Primer: če bi bila naša uporabniška koda enaka 123456 in bi obstajal prvi testni primer, kakršen je prikazan na gornji sliki, bi lahko oddali spodnjo izhodno datoteko.
123456 Zlaganje 1 4 7 9 9 2 0 9 9 2 2 0 0 9 2 9 9 9 0 2 0 5 0 2 0 5 5 2 2 5 0
To ustreza prvemu od treh razporedov z ene od gornjih slik; obseg dobljenega lika je 34.
Vhodni podatki
- [novo] zlaganje.in — datoteka z vsemi vhodnimi podatki za to nalogo.
Registracija
Preden lahko oddajaš svoje rešitve, se prijavi prek spodnjega obrazca. Dodelili ti bomo enolično uporabniško kodo, ki jo boš potreboval(a) za pripravo svojih izhodnih datotek.
Opomba: pri tej nalogi lahko sodeluje kdorkoli, ne glede na starost, izobrazbo, itd. Objavili bomo rezultate vseh tekmovalcev, za morebitne praktične nagrade pa pridejo v poštev le srednješolci/ke in študentje/ke.