Srednješolsko tekmovanje ACM iz računalništva in informatike
Pokrajina iz kock
To je „off-line naloga“. Na tej spletni strani je objavljen opis naloge in testni primeri. Svoje rešitve lahko pošlješ prek obrazca na tej strani kadarkoli do vključno 26. marca 2021 (dan pred tekmovanjem).
- Kratek opis naloge na tej strani.
- Podroben opis naloge in oblike vhodnih ter izhodnih datotek.
- Vhodne datoteke.
- Registracija (preden lahko oddajaš svoje rešitve).
- Obrazec za oddajo tvojih rešitev.
- Najboljši doslej oddani rezultati za posamezni testni primer.
- Razvrstitev tekmovalcev v skupnem seštevku.
Opis naloge
Iz kock, podobnih lego kockam, bi radi sestavili trodimenzionalni model pokrajine. Pokrajina je opisana z višinskim zemljevidom oz. tlorisom; območje, ki nas zanima, ima v tlorisu obliko pravokotnika, ki ga v mislih razdelimo na karirasto mrežo enotskih kvadratov. Ta mreža ima w stolpcev in h vrstic. Za vsako celico mreže je podana višina pokrajine v tej celici, recimo v[x, y] za celico na preseku stolpca x in vrstice y. Vse te višine so cela števila, večja ali enaka 0.
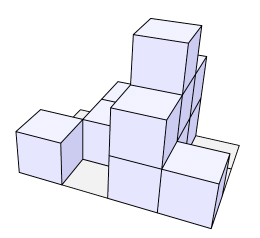
Primer višinskega zemljevida (w = 4, h = 3) in pripadajoče pokrajine:
|
|
„Kocke“, iz katerih sestavljamo naš model pokrajine, so v resnici kvadri različnih velikosti. Možne velikosti kvadrov so podane, za vsako velikost pa imamo na voljo neomejeno število kvadrov tiste velikosti. Kvadre moramo zlagati tako, da se med seboj ne prekrivajo, da ne štrlijo ven iz pokrajine in da pokrijejo celotno pokrajino. Kvadre smemo vrteti v korakih po 90° okrog navpične osi (torej osi z), tako da lahko na primer kvader velikosti ax × ay × az uporabimo tudi kot kvader velikosti ay × ax × az.
Tvoja naloga je sestaviti tak model pokrajine, ki ustreza tem omejitvam in pri tem porabi čim manj kvadrov.
Primer: recimo, da imamo višinski zemljevid z zgornje slike in da so na voljo kvadri naslednjih velikosti: 1 × 1 × 1, 2 × 1 × 1, 3 × 1 × 1, 1 × 1 × 2.
Naslednji dve sliki kažeta dva izmed možnih načinov, kako lahko iz kvadrov takih velikosti sestavimo pokrajino s tega višinskega zemljevida (kvadre na slikah smo pobarvali z različnimi barvami, vendar le zato, da se jih lažje razloči, drugače pa barve ne pomenijo ničesar posebnega):
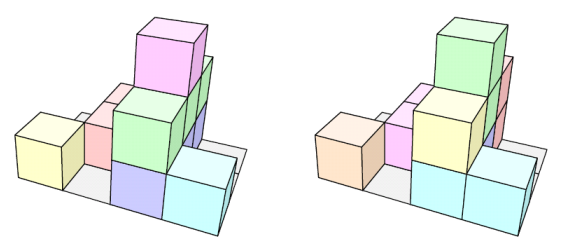
Rešitev na levi sliki sestavlja 6 kvadrov, rešitev na desni sliki pa 7 kvadrov, zato je leva rešitev boljša od desne.
- Podrobnejši opis naloge ter vhodnih in izhodnih datotek.
- Vhodne datoteke.
- Registracija.
Obrazec za oddajo rešitev
(Oddaja rešitev je možna do vključno 26. marca 2021.)
Najboljše doslej oddane rešitve
Skupni seštevek
V skupnem seštevku se za vsakega tekmovalca seštejejo njegove točke z vseh testnih primerov.
| Ime in priimek | Rezultat |
|---|---|
| Samo Kralj | 258 |
| Domen | 213 |
| Jošt Smrtnik | 182 |
| Gregor Kikelj | 170 |
[H kazalu. | Na vrh te strani. | Imate vprašanje ali komentar?]